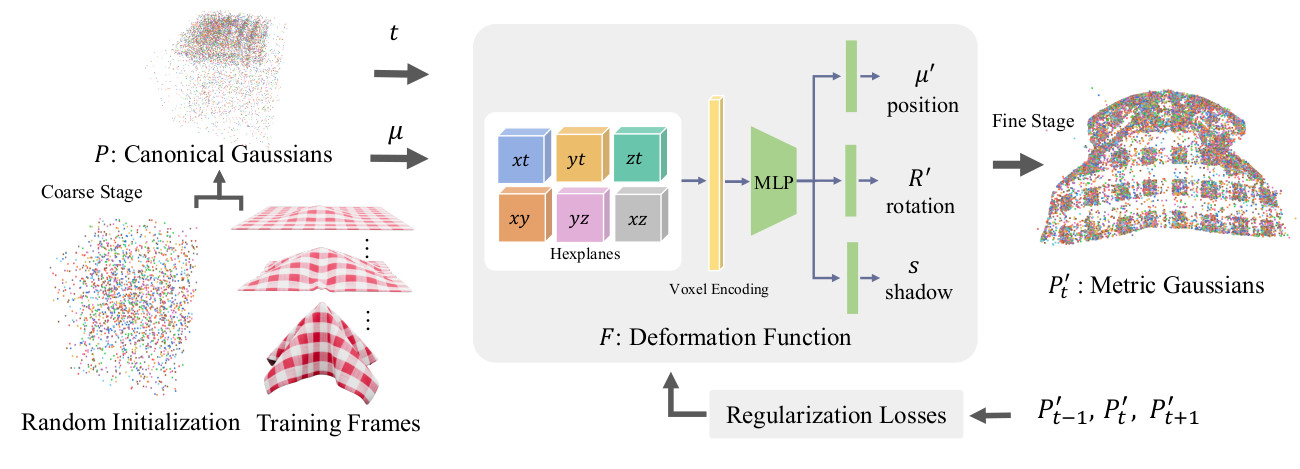
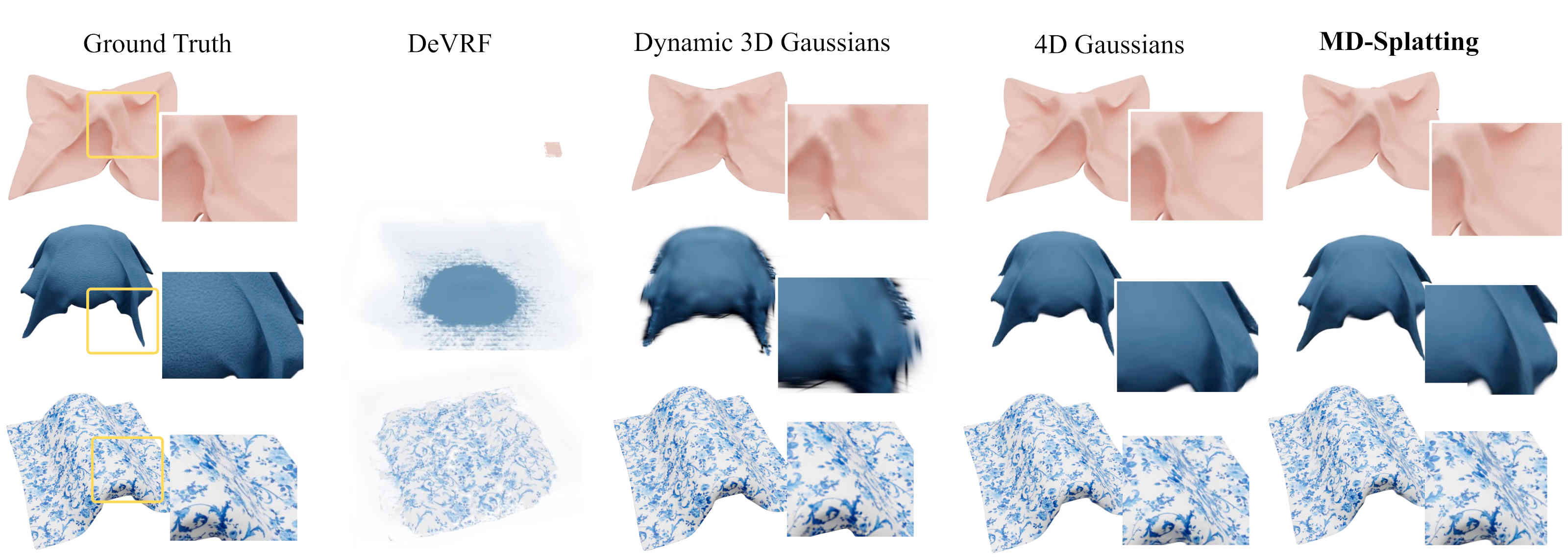
Accurate 3D tracking in highly deformable scenes with occlusions and shadows can facilitate new applications in robotics, augmented reality, and generative AI. However, tracking under these conditions is extremely challenging due to the ambiguity that arises with large deformations, shadows, and occlusions. We introduce MD-Splatting, an approach for simultaneous 3D tracking and novel view synthesis, using video captures of a dynamic scene from various camera poses. MD-Splatting builds on recent advances in Gaussian splatting, a method that learns the properties of a large number of Gaussians for state-of-the-art and fast novel view synthesis. MD-Splatting learns a deformation function to project a set of Gaussians with non-metric, thus canonical, properties into metric space. The deformation function uses a neural-voxel encoding and a multilayer perceptron (MLP) to infer Gaussian position, rotation, and a shadow scalar. We enforce physics-inspired regularization terms based on local rigidity, conservation of momentum, and isometry, which leads to trajectories with smaller trajectory errors. MD-Splatting achieves high-quality 3D tracking on highly deformable scenes with shadows and occlusions. Compared to state-of-the-art, we improve 3D tracking by an average of 23.9 %, while simultaneously achieving high-quality novel view synthesis. With sufficient texture such as in scene 6, MD-Splatting achieves a median tracking error of 3.39 mm on a cloth of 1 × 1 meters in size.
MD-Splatting maps a set of Gausians with canonical properties to metric space using a deformation function F. The deformation function takes in the position of a Gaussian x and a queried timestamp t, to infer shadow s, rotation R' and metric position x'. The metric positions and rotations are used to regularize the deformation function to incentivize more physically plausbile trajectories.
